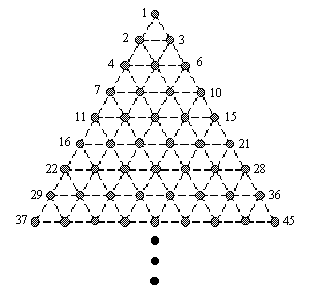
Note that if we number the points from left to right and top to bottom, then groups of these points form the vertices of certain geometric shapes. For example, the sets of points {1,2,3} and {7,9,18} are the vertices of triangles, the sets {11,13,26,24} and {2,7,9,18} are the vertices of parallelograms, and the sets {4,5,9,13,12,7} and {8,10,17,21,32,34} are the vertices of hexagons.

Write a program which will repeatedly accept a set of points on this triangular grid, analyze it, and determine whether the points are the vertices of one of the following "acceptable" figures: triangle, parallelogram, or hexagon. In order for a figure to be acceptable, it must meet the following two conditions:

1. Each side of the figure must coincide with an edge in the grid.
2. All sides of the figure must be of the same length.

Input and Output

For each point set in the input file, your program should deduce from the number of points in the set which geometric figure the set potentially represents; e.g., six points can only represent a hexagon, etc. The output must be a series of lines listing each point set followed by the results of your analysis.

Sample Solution

Sample Input

1 2 3	
11 13 29 31
26 11 13 24
4 5 9 13 12 7
1 2 3 4 5
47	
11 13 23 25

Sample Output

1 2 3 are the vertices of a triangle
11 13 29 31 are not the vertices of an acceptable figure
26 11 13 24 are the vertices of a parallelogram
4 5 9 13 12 7 are the vertices of a hexagon
1 2 3 4 5 are not the vertices of an acceptable figure
47 are not the vertices of an acceptable figure
11 13 23 25 are not the vertices of an acceptable figure