Not an official ACM page
[Problem C
| 1992 ACM finals problem set
| My ACM problem archive
| my home page]
1992 ACM Scholastic Programming Contest Finals
sponsored by AT&T EasyLink Services
Problem B
Getting in Line
Computer networking requires that the computers in the network be
linked. This problem considers a "linear" network in which the
computers are chained together so that each is connected to exactly
two others except for the two computers on the ends of the chain which
are connected to only one other computer. A picture is shown
below. Here the computers are the black dots and their locations in
the network are identified by planar coordinates (relative to a
coordinate system not shown in the picture). Distances between linked
computers in the network are shown in feet.
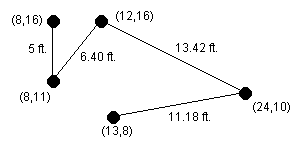
For various reasons it is desirable to minimize the length of cable
used. Your problem is to determine how the computers should be
connected into such a chain to minimize the total amount of cable
needed. In the installation being constructed, the cabling will run
beneath the floor, so the amount of cable used to join 2 adjacent
computers on the network will be equal to the distance between the
computers plus 16 additional feet of cable to connect from the floor
to the computers and provide some slack for ease of installation.
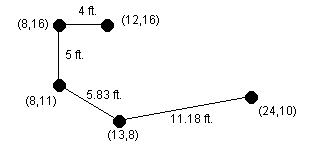
The picture below shows the optimal way of connecting the computers
shown above, and the total length of cable required for this
configuration is (4+16)+ (5+16) + (5.83+16) + (11.18+16) = 90.01 feet.
Input
The input file will consist of a series of data sets. Each data set
will begin with a line consisting of a single number indicating the
number of computers in a network. Each network has at least 2 and at
most 8 computers. A value of 0 for the number of computers indicates
the end of input. After the initial line in a data set specifying the
number of computers in a network, each additional line in the data set
will give the coordinates of a computer in the network. These
coordinates will be integers in the range 0 to 150. No two computers
are at identical locations and each computer will be listed once.
Output
The output for each network should include a line which tells the
number of the network (as determined by its position in the input
data), and one line for each length of cable to be cut to connect each
adjacent pair of computers in the network. The final line should be a
sentence indicating the total amount of cable used. In listing
the lengths of cable to be cut, traverse the network from one end to
the other. (It makes no difference at which end you start.)
Use a format similar to the one shown in the sample output, with a
line of asterisks separating output for different networks and with
distances in feet printed to 2 decimal places.
Sample Input
6
5 19
55 28
38 101
28 62
111 84
43 116
5
11 27
84 99
142 81
88 30
95 38
3
132 73
49 86
72 111
0
Sample Output
**********************************************************
Network #1
Cable requirement to connect (5,19) to (55,28) is 66.80 feet.
Cable requirement to connect (55,28) to (28,62) is 59.42 feet.
Cable requirement to connect (28,62) to (38,101) is 56.26 feet.
Cable requirement to connect (38,101) to (43,116) is 31.81 feet.
Cable requirement to connect (43,116) to (111,84) is 91.15 feet.
Number of feet of cable required is 305.45.
**********************************************************
Network #2
Cable requirement to connect (11,27) to (88,30) is 93.06 feet.
Cable requirement to connect (88,30) to (95,38) is 26.63 feet.
Cable requirement to connect (95,38) to (84,99) is 77.98 feet.
Cable requirement to connect (84,99) to (142,81) is 76.73 feet.
Number of feet of cable required is 274.40.
**********************************************************
Network #3
Cable requirement to connect (132,73) to (72,111) is 87.02 feet.
Cable requirement to connect (72,111) to (49,86) is 49.97 feet.
Number of feet of cable required is 136.99.
This page maintained by
Ed Karrels.
Last updated September 20, 1999


