Not an official ACM page
[Problem B
| 1995 ACM finals problem set
| My ACM problem archive
| my home page]
1995 ACM Scholastic Programming Contest Finals
sponsored by Microsoft ®
Problem A
Jill's Bike
Jill Bates hates climbing hills. Jill rides a bicycle everywhere she
goes, but she always wants to go the easiest and shortest way
possible. The good news is that she lives in Greenhills, which has all
its roads laid out in a strictly rectangular grid--east-west roads are
streets; north-south roads are avenues and the
distance between any two adjacent grid points is the same. The bad
news is that Greenhills is very hilly and has many one-way roads.
In choosing a route between where she starts and where she ends, Jill
has three rules:
- Avoid any climb of more than 10 meters between adjacent grid points.
- Never go the wrong way on a one-way road.
- Always travel the shortest possible route.
Your program should help Jill find an acceptable route.
Input
The input file contains data in the following form:
- The first line contains two integers, separated by one or more
spaces. The first integer n represents the number of streets,
and the second integer m represents the number of avenues,
1<= n <=20, 1<= m <=20.
- The next n lines contain the altitudes of grid
points. Each line represents a street and contains a sequence of
m integers separated by one or more spaces. These integers
represent the altitude in meters of the grid points along that
street. Even if a particular street and avenue have no intersection,
the altitude is still given for that grid point.
- One or more lines follow that define the one-way roads. Each road
is represented by two pairs of integers, separated by one or more
spaces, in the form:
street avenue street avenue
The first street and avenue define the starting point of the road and
the second pair define the ending point. Since Greenhills is a strict
grid, if the two points are not adjacent in the grid, the road passes
through all the intervening grid points. For example,
5 7 5 8
5 8 5 9
5 9 5 10
represents roads 5-7 to 5-8, 5-8 to 5-9, and 5-9 to 5-10. Road
definitions are terminated by a line containing four zeroes in the
above format.
- Finally, one or more lines will follow that contain pairs of grid
points between which Jill wants to find an optimal path, in the form:
street avenue street avenue
As before, the integer pairs are separated by one or more spaces. The
end of the input set is defined by a line containing four zeroes,
formatted as before.
You may assume that all street and avenue numbers are within the
bounds defined by the first line of input, and that all road
definitions are strictly north-south or east-west.
Output
For each path query in the input file, output a sequence of grid
points, from the starting grid point to the ending grid point, which
meets Jill's three rules. Output grid points as
'street-avenue' separated by the word 'to'. If
there is more than one path that meets Jill's criteria, any such path
will be acceptable. If no route satisfies all the criteria, or if the
starting and ending grid points are the same, output an appropriate
message to that effect. Output a blank line between each output set.
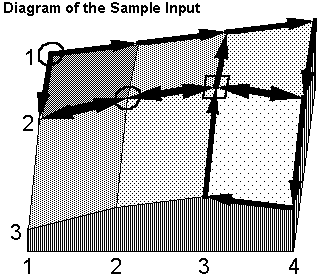
Sample Input
3 4
10 15 20 25
19 30 35 30
10 19 26 20
1 1 1 4
2 1 2 4
3 4 3 3
3 3 1 3
1 4 3 4
2 4 2 1
1 1 2 1
0 0 0 0
1 1 2 2
2 3 2 3
2 2 1 1
0 0 0 0
Output for the Sample Input
1-1 to 1-2 to 1-3 to 1-4 to 2-4 to 2-3 to 2-2
To get from 2-3 to 2-3, stay put!
There is no acceptable route from 2-2 to 1-1.
This page maintained by
Ed Karrels.
Last updated September 20, 1999

