A simple solitaire card game called 10-20-30 uses a standard deck of 52 playing cards in which suit is irrelevant. The value of a face card (king, queen, jack) is 10. The value of an ace is one. The value of each of the other cards is the face value of the card (2, 3, 4, etc.). Cards are dealt from the top of the deck. You begin by dealing out seven cards, left to right forming seven piles. After playing a card on the rightmost pile, the next pile upon which you play a card is the leftmost pile.

For each card placed on a pile, check that pile to see if one of the following three card combinations totals 10, 20, or 30.

1. the first two and last one,
2. the first one and the last two, or
3. the last three cards.

If so, pick up the three cards and place them on the bottom of the deck. For this problem, always check the pile in the order just described. Collect the cards in the order they appear on the pile and put them at the bottom of the deck. Picking up three cards may expose three more cards that can be picked up. If so, pick them up. Continue until no more sets of three can be picked up from the pile.

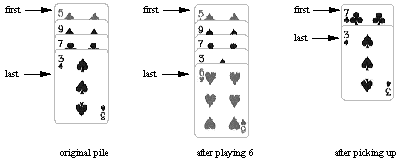
For example, suppose a pile contains 5 9 7 3 where the 5 is at the first card of the pile, and then a 6 is played. The first two cards plus the last card (5 + 9 + 6) sum to 20. The new contents of the pile after picking up those three cards becomes 7 3. Also, the bottommost card in the deck is now the 6, the card above it is the 9, and the one above the 9 is the 5.

If a queen were played instead of the six, 5 + 9 + 10 = 24, and 5 + 3 + 10 = 18, but 7 + 3 + 10 = 20, so the last three cards would be picked up, leaving the pile as 5 9.

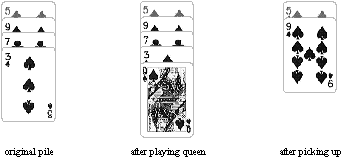
If a pile contains only three cards when the three sum to 10, 20, or 30, then the pile "disappears" when the cards are picked up. That is, subsequent play skips over the position that the now-empty pile occupied. You win if all the piles disappear. You lose if you are unable to deal a card. It is also possible to have a draw if neither of the previous two conditions ever occurs.

Write a program that will play games of 10-20-30 given initial card decks as input.

---

Input

---

Output

---

Sample Input

2 6 5 10 10 4 10 10 10 4 5 10 4 5 10 9 7 6 1 7 6 9 5 3 10 10 4 10 9 2 1 
10 1 10 10 10 3 10 9 8 10 8 7 1 2 8 6 7 3 3 8 2
4 3 2 10 8 10 6 8 9 5 8 10 5 3 5 4 6 9 9 1 7 6 3 5 10 10 8 10 9 10 10 7 
2 6 10 10 4 10 1 3 10 1 1 10 2 2 10 4 10 7 7 10
10 5 4 3 5 7 10 8 2 3 9 10 8 4 5 1 7 6 7 2 6 9 10 2 3 10 3 4 4 9 10 1 1 
10   5 10 10 1 8 10 7 8 10 6 10 10 10 9 6 2 10 10
0

---

Output for the Sample Input

Win : 66
Loss: 82
Draw: 73