Not an official ACM page
[Problem F | 1996 ACM finals problem set | My ACM problem archive | my home page]

1996 ACM Scholastic Programming Contest Finals

Problem E

Pattern Matching Prelims

Input file: pattern.in

Some algorithms for optical character recognition compare a scanned image with templates of "perfect" characters. Part of the difficulty with such comparisons is deciding where to start the comparison. This is because the characters in the scanned image are subject to noise and distortion, resulting in changes in size, position, and orientation. A procedure that is sometimes used to deal with changes in position matches the "center of gravity" of the scanned character and the templates against which it is compared. In this problem you are to determine the "centers of gravity" of scanned images of characters.

For our purposes, a scanned image will be a rectangular array of real numbers, each of which represents the gray-scale value of a point in a scanned image. Each gray-scale value will be between 0 (representing a totally white region) and 1 (representing a totally black region). The array will have no more than 25 rows and 25 columns.

The center of gravity is a particular element of an array. Suppose a center of gravity is in the ith row and jth column. Then the difference between the sum of the elements of the two array portions above and below the ith row is minimal. Likewise, the difference of the sums of the elements in the two array portions to the left and to the right of the jth column is minimal.

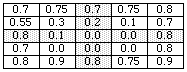
Consider the array shown below, which might have resulted from scanning a lower case "to." The center of gravity for this array is uniquely in row 3, column 3. The difference of the sum of the elements in each array portion formed by ignoring the third row is 0.1 (the sums are 5.55 and 5.65). The difference of the sum of each array portion formed by ignoring the third column is 0.0 (the sums are both 5.60).

Input

The input will consist of a sequence of scanned character images. Input for each image will begin with two integers specifying the number of rows and columns in the scanned data. This will be immediately followed by the scanned gray-scale data given in row-major order. A pair of zeroes will follow the data for the last input image.

Output

For each input character image, display its number (they are sequentially numbered starting with 1) and the row and column corresponding to the center of gravity. If there is more than one center of gravity, the one with the largest row and column should be displayed. The sample that follows illustrates a reasonable output format.

Sample Input

5 5
0.1 0.2 0.1 0.2 0.1
0.1 0.2 0.3 0.1 0.1
0.2 0.3 0.1 0.1 0.3
0.4 0.1 0.1 0.1 0.2
0.2 0.2 0.3 0.3 0.1

5 10
0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1
0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2
0.3 0.3 0.3 0.3 0.3 0.3 0.3 0.3 0.3 0.3
0.4 0.4 0.4 0.4 0.4 0.4 0.4 0.4 0.4 0.4
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.6

0 0

Output for the Sample Input

Case 1: center at (3, 3)
Case 2: center at (4, 6)

This page maintained by Ed Karrels.
Last updated September 20, 1999