Not an official ACM page
[ Problem G
| 1998 ACM Finals problem set
| My ACM problem archive
| my home page]
The 1998 22nd Annual
acm
International Collegiate
Programming Contest World Finals
sponsored by IBM
Problem F
Polygon Intersections
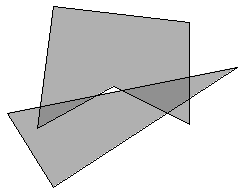
Most drawing or illustration programs have simple tools for creating
polygon objects. The better ones can find the regions that are the
intersections of two polygons. The picture below shows two polygons,
one is a pentagon and the other is a triangle. Their intersection
consists of the two dark regions.
IBM has just hired you as a member of a programming team that will
create a very sophisticated drawing/illustration program. Your task is
to write the part of the program that deals with polygon
intersections. Your boss has told you to delay work on the user
interface and focus only on the geometric representations of the
intersections. A polygon in the Cartesian plane can be represented by
a sequence of points that are its vertices. The vertices in the
sequence appear in the order in which they are visited when traveling
clockwise around the polygon's boundary; so any two adjacent vertices
in the sequence are the endpoints of a line segment that is one of the
polygon's sides. The last and the first vertices in the sequence are
also endpoints of a side. Vertices are identified by their
x- and y- coordinates. Assume the following about
each polygon.
- No point will occur as a vertex (on the same polygon) more than once.
- Two sides can intersect only at a common endpoint (vertex).
- The angle between any two sides with a common vertex has a measure that
is greater than 0 and less than 360.
- The polygon has at least 3 vertices.
The intersection of two polygons consists of 0 or more connected
regions. Your problem is to take two polygons and determine the
regions of their intersection that are polygons satisfying the
criteria above.
Input
The input contains several data sets, each consisting
of two polygons. Each polygon appears as a sequence of numbers:
n x1 y1 x2 y2 ... xn yn
where the integer n is the number of vertices of the polygon,
and the real coordinates (x1,
y1) through (xn,
yn) are the boundary vertices. The end of input is
indicated by two 0's for the values of n. These two 0's
merely mark the end of data and should not be treated as an additional
data set.
Output
For each data set, your program should output its
number (Data set 1, Data set 2, etc.), and the number of regions in
the intersection of its two polygons. Label each region in the data
set (Region 1, Region 2, etc.) and list its vertices in the order they
appear when they are visited going either clockwise or
counterclockwise around the boundary of the region. The first vertex
printed should be the vertex with the smallest x-coordinate
(to break ties, use the smallest y-coordinate). No region
may include degenerate parts (consisting of adjacent sides whose angle
of intersection is 0). If the three endpoints of two adjacent sides
are collinear, the two sides should be merged into a single
side. Print each vertex in the standard form (x, y),
where x and y have two digits to the right of the
decimal.
The following sample input contains exactly one data set. (The data
set corresponds to the illustration at the beginning of this problem
description.)
Sample Input
3 2 1 0.5 3.5 8 5
5 1.5 3 2 7 6.5
6.5
6.5 3.25 4 4.5
0
0
Output for the Sample Input
Data Set 1
Number of intersection regions: 2
Region 1:(1.50,3.00)(1.59,3.72)(3.25,4.05)
Region 2:(4.43,4.29)(6.50,4.70)(6.50,4.00)(5.86,3.57)
This page maintained by
Ed Karrels.
Last updated September 8, 1999

