Not an official ACM page
[ Problem C | 1999 ACM Finals problem set | My ACM problem archive | my home page]
The 23rd Annual
ACM International Collegiate
Programming Contest
WORLD FINALS
sponsored by IBM


Problem B
Bullet Hole


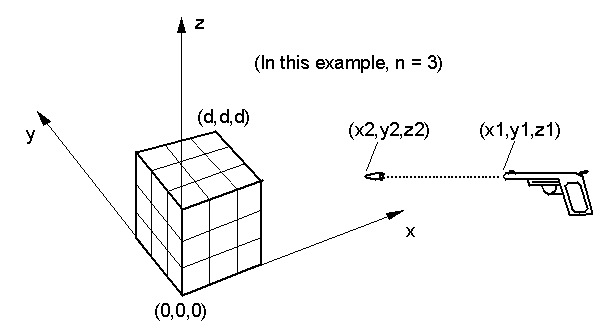
Cube and gun diagram

A cube is suspended in space. A Cartesian coordinate system is defined with its origin at one of the bottom corners of the cube, as shown in the figure. The cube has side dimension d, so its opposite corners are at coordinates (0, 0, 0) and (d, d, d). The positive z-direction of the coordinate system is "up" with respect to gravity.

The interior of the cube contains partitions with uniform spacing in each dimension, so that the cube is partitioned into n3 mini-cubes of equal size. The partitions are thin and watertight, and each mini-cube is filled with water. The total volume of water in all the minicubes is d3.

A gun fires a bullet which may hit the cube. The muzzle of the gun is at the point (x1, y1, z1). The point (x2, y2, z2) is a point on the bullet's path that defines the direction of the bullet. The bullet does not shatter the cube, but wherever the bullet touches a side or interior partition of the cube, it makes a small hole. Bullet holes may be made in the sides, edges, or corners of the interior mini-cubes. Water, influenced by gravity, may leak through these small holes. All the water that leaks out of the large cube is collected and measured.

Input

The input data set consists of several trials. Each trial is described by eight integers. The first integer is n (n <= 50), as described above. The second integer is d (d <= 100). The remaining six integers-x1, y1, z1, x2, y2, z2-represent the origin and a point on the path of the bullet (-100 <= x1, y1, z1, x2, y2, z2 <= 100). The origin and the point on the path of the bullet are not the same. After the last trial, the integer 0 terminates the data set.

Output

Your program must compute the total volume of water that leaks out of the large cube. For each trial, print the trial number, the notation Volume =, and the total volume of water accurate to two digits to the right of the decimal point. Print a blank line between trials.

Note

In this problem, two real numbers are considered equal if they are less than 10-6 apart.

Sample Input

 5   25     5  15   0     5  15 100
 3   30     0 -35   0     3 -25   3
10   16     8  17  11    12  19   6
 0

Output for the Sample Input

Trial 1, Volume = 2500.00

Trial 2, Volume = 1950.00

Trial 3, Volume = 0.00
This page maintained by Ed Karrels.
Last updated December 7, 1999