Not an official ACM page
[ Problem E
| 1992 ACM East-Central Regional problem set
| My ACM problem archive
| my home page]

 Writings discovered inside the walls of the Great Pyramids have often
revealed the ancient Egyptian's affinity for mathematical logic and
problem solving.
Writings discovered inside the walls of the Great Pyramids have often
revealed the ancient Egyptian's affinity for mathematical logic and
problem solving.
Recently, a team of archaeologists returning from an expedition to the
pyramids brought back several examples of ancient hieroglyphics which,
when translated into their English equivalents, provided further
evidence of their mathematical prowess.
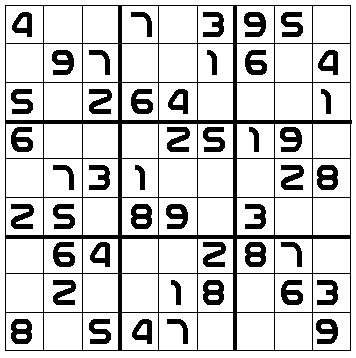
The grid at the left, one of many derived from the hieroglyphics, was
presented to a team of mathematical scholars for their analysis. After
careful study, they determined that this grid represented a mathematical
challenge. To the best of their knowledge, the goal seems to be to fill
in the empty spaces with the numbers from one through nine, subject
to the following constraints:
- numbers initially appearing inthe grid are fixed and cannot be moved;
- each number may appear only once in each horizontal row and vertical column; and
- each number may appear only once in each smaller square of nine as
delineated by the heavier lines in the grid diagram
In an effort to better understand this ancient civilization (and to use the
technology of the present to address the challenges of the past), your team
has decided to develop a program that will "complete the squares", so
to speak, found in the pyramids.
Input
The input will consist of a series of Egyptian squares. On the first
line of the input file will be a single integer stating the number of
Egyptian squares in the dataset. This will be followed by data for
that many Egyptian squares. Each Egyptian square will consist of nine
lines of nine single-digit integers that are separated by spaces. In
each Egyptian square, at least four fixed numbers in each row, column,
and smaller square of nine will be provided, with the empty spaces
denoted by the integer zero. Every number from 1 to 9 will appear at
least once in each Egyptian square as a fixed digit. Only valid data
will appear in the input file.
Output
Since the Egyptians prided themselves on their mathematical abilities, it is
safe to assume that each square will have at least one solution. Should multiple
answers be possible, your program may output any of these answers
(but only one). Each Egyptian square is to be assigned an identification
number, beginning with square #1. A heading of EGYPTIAN SQUARE #n
should be output, followed by a blank line, and the lines showing the solved square. The numbers within an Egyptian square should be output right-justified in a field width of two character positions. The output for one Egyptian square is to be separated from the output of the next Egyptian square by a blank line. Refer to the example on the next page.
Sample Input
2
4 0 0 7 0 3 9 5 0
0 9 7 0 0 1 6 0 4
5 0 2 6 5 0 0 0 1
6 0 0 0 2 5 1 9 0
0 7 3 1 0 0 0 2 8
2 5 0 8 9 0 3 0 0
0 6 4 0 0 2 8 7 0
0 2 0 0 1 8 0 6 3
8 0 5 4 7 0 0 0 9
0 9 0 1 0 0 0 4 7
4 0 1 0 2 0 0 0 5
6 0 0 0 8 7 9 0 0
0 6 5 9 0 0 0 2 0
0 0 8 0 5 6 7 0 0
1 0 0 0 0 3 5 0 6
2 0 0 0 9 4 0 5 0
0 8 0 3 0 0 0 7 9
0 3 9 5 0 0 2 0 0
Output for the Sample Input
EGYPTIAN SQUARE #1
4 1 6 7 8 3 9 5 2
3 9 7 2 5 1 6 8 4
5 8 2 6 4 9 7 3 1
6 4 8 3 2 5 1 9 7
9 7 3 1 6 4 5 2 8
2 5 1 8 9 7 3 4 6
1 6 4 9 3 2 8 7 5
7 2 9 5 1 8 4 6 3
8 3 5 4 7 6 2 1 9
EGYPTIAN SQUARE #2
8 9 2 1 3 5 6 4 7
4 7 1 6 2 9 3 8 5
6 5 3 4 8 7 9 1 2
3 6 5 9 7 1 4 2 8
9 4 8 2 5 6 7 3 1
1 2 7 8 4 3 5 9 6
2 1 6 7 9 4 8 5 3
5 8 4 3 6 2 1 7 9
7 3 9 5 1 8 2 6 4
This page maintained by
Ed Karrels.
Last updated December 12, 1999

 Writings discovered inside the walls of the Great Pyramids have often
revealed the ancient Egyptian's affinity for mathematical logic and
problem solving.
Writings discovered inside the walls of the Great Pyramids have often
revealed the ancient Egyptian's affinity for mathematical logic and
problem solving.