
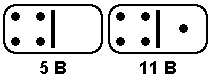
Consider a standard set of double-six dominoes with each piece in the set (each
bone) assigned an identification number as shown below:

A popular diversion among domino layers involves laying several of the bones form the set (selected at random) end-to-end, and then eliminating adjacent pairs of cominoes (from left to right) which touch at the same pip value. Consider the example with six dominoes shown below.


The original draw resulted in these six dominoes. Note that when each domino is aligned, it may appear in either its forward or its backward orientation (the table above shows the forward orientations of all non-doubles). Play begins from the left end and returns to the left end after any pair of dominoes is eliminated. In this case, domino #12 (in its forward orientation) and domino #17 (in its backward orientation) are eliminated from the row since they touch each other with 5 pips. The row is collapsed and play begins again at the left end. This time, dominoes #15 and #20 (both in their forward orientations) are eliminated since they touch each other with 3 pips. The row is again collapsed. Since no further eliminations can be made, the game ends. Note that dominoes #20 and #11 could not be eliminated since they were never the left-most pair.
Write a program that will accept a row of domino I. D. numbers and their orientations, and carry out any such successive left-most eliminations until no more are possible.
F or B) which indicates the
domino's orientation (forward or backward, respectively). The
terminating record will always be 0 F. Although it is
unnecessary information for doubles (dominoes with the same number of
pips on each end), an (arbitrary) orientation of F or
B will still be part of that domino's record. Each
domino record (including the terminating record) will appear on a line
by itself. The first domino in each set is the leftmost, while the
one preceding the terminator is the rightmost. You may assume that
each domino will appear at most once in each dataset and that all data
will be valid.
RESULTS OF ELIMINATIONS and will
have two blank lines separating it form the rest of the report. The
remainder of the report will consist of one line for each domino
dataset. Each of these lines will contain the domino I. D. numbers
which remain in each set after all eliminations have been carried out
(in sequence from left to right). Each domino I. D. number should be
printed in a field that is exactly the I. D. number's width and
followed by exactly one space. Domino orientations are not
to be printed. One blank line should appear between the results for
each dataset. Should it ever be possible to eliminate every domino in
a dataset, the line DATASET CLEARED hsould be printed in
place of any domino I. D. numbers.
5 B 15 F 12 F 17 B 20 F 11 B 0 F 18 F 22 B 0 F 23 F 12 B 2 B 4 F 15 B 20 B 19 B 7 B 6 F 0 F
RESULTS OF ELIMINATIONS 5 11 DATASET CLEARED 19