Not an official ACM page
[Problem B
| 1995 East-Central problem set
| My ACM problem archive
| my home page]
1995 East-Central Regionals
ACM International Collegiate programming Contest
sponsored by Microsoft
Problem A - Pi
Professor Robert A. J. Matthews of the Applied Mathematics and Computer Science Department at the
University of Aston in Birmingham, England has recently described howthe positions of stars across the
night skymay be used to deduce a surprisingly accurate value of 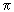 .This result
followed from the application of certain theorems in number theory.
.This result
followed from the application of certain theorems in number theory.
Here, we don'thave the night sky, but can use the same theoretical basis to form an estimate for 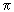 :
:
Given any pair of whole numbers chosen from a large, random collection of numbers, the
probability that the twonumbers have nocommon factor other than one (1) is
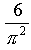
For example, using the small collection of numbers: 2, 3, 4, 5, 6; there are 10 pairs that can be formed:
(2,3), (2,4), etc. Six of the 10 pairs: (2,3), (2,5), (3,4), (3,5), (4,5) and (5,6) have nocommon factor other
than one. Using the ratio of the counts as the probability we have:
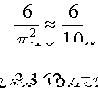
In this problem, you'll receive a series of data sets. Each data set contains a set of pseudo-random positive
integers. For each data set, find the portion of the pairs which may be formed that have no common factor
other than one (1), and use the method illustrated above toobtain an estimate for 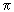 .
Report this estimate for each data set.
.
Report this estimate for each data set.
Input
The input consists of a series of data sets.
The first line of each data set contains a positive integer value, N, greater than one (1) and less than 50.
There is one positive integer per line for the next N lines that constitute the set for which the pairs are to be
examined. These integers are each greater than 0 and less than 32768.
Each integer of the input stream has its first digit as the first character on the input line.
The set size designator, N, will be zero to indicate the end of data.
Output
A line with a single real value is to be emitted for each input data set encountered.
This value is the estimate for 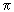 for the data set. The default real/float output format should be used. Answers must be within
0.1% of the correct answer.
For some data sets, it may be impossible to estimate a value for
for the data set. The default real/float output format should be used. Answers must be within
0.1% of the correct answer.
For some data sets, it may be impossible to estimate a value for 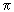 .This occurs when there are no pairs
without common factors. In these cases, emit the single-line message:
.This occurs when there are no pairs
without common factors. In these cases, emit the single-line message:
No estimate for this data set.
exactly, starting with the first character, "N", as the first character on the line.
Sample Input
5
2
3
4
5
6
2
13
39
0
Output for the Sample Output
3.162
No estimate for this data set.
This page maintained by
Ed Karrels.
Last updated November 6, 1997
![]() :
:
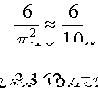
![]() .
Report this estimate for each data set.
.
Report this estimate for each data set.