"What's the matter, Valentine?" Martin asked.
"My presentation to the SSC. They all really liked the graphical displays of the criteria and the selection process," Valentine grudgingly admitted. "But, Prof. Everett pointed out that the criteria would change over time and since we will be using the machine over several years, that we needed to take that into account as well."
"Maybe you could make separate graphs for each year?" suggested Martin.
"That's what I said to Prof. Everett, but she didn't think that would be sufficient --- it would only pick the best machine for a particular year."
As Valentine silently pondered her problem, Jake Briggs, one of Valentine's CS classmates, joined Martin and Valentine at their table. "What's up?" he asked. Valentine explained her dilemma.
"Simple," Jake mumbled through bites of his club sandwich. "Make three-dimensional shapes, using time as the third axis. The computer with the largest volume wins."
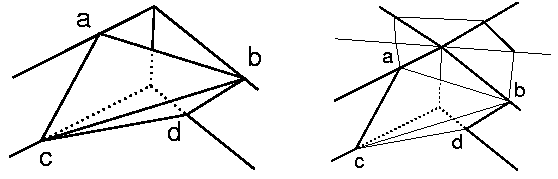
Valentine sketched out a perspective drawing of such a volume as well as a detail of a single quadrant. "What do we do here at the edges of the axes? There are four points." Valentine pointed to the points a, b, c, and d in her drawing of the quadrant.

"Just use two planes, one determined by a, b, and c, and the other determined by b, and c, and d."
"Whoa! Problem!" exclaimed Martin. "Those volume things are way too complicated for slideware. You'll just confuse everyone."
"No problem," Jake said. "We can use our virtual reality cave over in the JFK building. It even has tactile feedback gloves. The committee members can touch the volumes if they want."
The rest of the input will consist of sequences of possible configurations of supercomputers; each line will contain n floating point values. The supercomputer configurations will be grouped in sets of y, i.e., the first y lines (after the initial line of two integers) will be the yearly configurations for the first computer. The next y lines will be the yearly configurations for the second computer, etc.
The first number on the input line corresponds to the value on the first axis, the second number corresponds to the value on the second axis, and so on.
The final line of input will contain n floating point zeros.
In case of a tie (i.e., multiple configurations are given that produce a polygon of equal volume), output the one with the lowest configuration number.
5 2 1.2 2.3 3.4 4.5 5.6 0.2 3.3 4.4 5.6 4.5 10.0 11.0 12.0 13.0 14.0 9.0 12.0 11.0 14.0 13.0 0.0 0.0 0.0 0.0 0.0
2 339.84