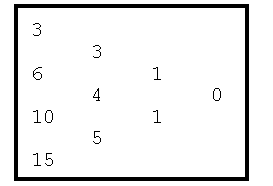
The original sequence of values appears in the first column of the table. Each entry in the second column of the table is formed by computing the difference between the adjacent entries in the first column. These values (in the second column) are called first differences. Each entry in the third column is similarly the difference between the adjacent entries in the second column; the third column entries are naturally called second differences. Computation of the last column in this example should now be obvious (but beware that this value is not always zero). Note that the last column will always contain only a single value. If we begin with a sequence of n values, the completed difference table will have n columns, with the single value in column n representing the single n-1st difference.

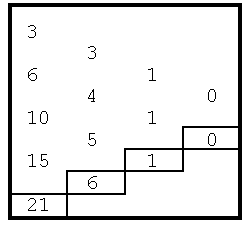
To extrapolate using a difference table we assume the n-1st differences are constant (since we have no additional information to refute that assumption). Given that assumption, we can compute the next entry in the n-2nd difference column, the n-3rd difference column, and so forth until we compute the next entry in the first column which, of course, is the next value in the sequence. The table below shows the four additional entries (in boxes) added to the table to compute the next entry in the example sequence, which in this case is 21. We could obviously continue this extrapolation process as far as desired by adding additional entries to the columns using the assumption that the n-1st differences are constant.

The input for this problem will be a set of extrapolation requests. For each request the input will contain first an integer n, which specifies the number of values in the sequence to be extended. When n is zero your program should terminate. If n is non-zero (it will never be larger than 10), it will be followed by n integers representing the given elements in the sequence. The last item in the input for each extrapolation request is k, the number of extrapolation operations to perform; it will always be at least 1. In effect, you are to add k entries to each column of the difference table, finally reporting the last value of the sequence computed by such extrapolation. More precisely, assume the first n entries (the given values) in the sequence are numbered 1 through n. Your program is to determine the n+kth value in the sequence by extrapolation of the original sequence k times. (Hint: no upper limit is given for k, and you might not be able to acquire enough memory to construct a complete difference table.)

Sample solution, C

Sample solution, Java

Try the Java solution:

---

Your browser does not support Java, or has disabled it.

---

Sample Input

4  3  6  10  15  1
4  3  6  10  15  2
3  2  4  6  20
6  3  9  12  5  18  -4  10
0

Expected Output

Term 5 of the sequence is 21
Term 6 of the sequence is 28
Term 23 of the sequence is 46
Term 16 of the sequence is 8412

Judge's Input Data

4 3 6 10 15 1
4 3 6 10 15 2
3 2 4 6 20
6 3 9 12 5 18 -4 10
10 1 1 1 1 1 1 1 1 1 1 1
10 1 2 1 2 1 2 1 2 1 2 1
10 1 2 1 2 1 2 1 2 1 2 6
10 1 1 1 1 1 1 1 1 1 1 30000
0

Expected Output from Judged runs

Term 5 of the sequence is 21
Term 6 of the sequence is 28
Term 23 of the sequence is 46
Term 16 of the sequence is 8412
Term 11 of the sequence is 1
Term 11 of the sequence is 513
Term 16 of the sequence is 27138
Term 30010 of the sequence is 1