In this problem you are required to recognize a small part of the PostScript language. Specifically, the commands listed below must be recognized. All commands will be given in lower-case letters. When the word number appears in the command description, a floating point value, with an optional sign and decimal point will be present in the input data. When two numbers appear in a command, the first refers to the x coordinate, and the second to the y coordinate. For simplicity, each command will appear on a line by itself, and a single blank will separate each component of the command. The end of line character will immediately follow each command, and a line with a single asterisk in column one will terminate the input.
number rotate
number represents the measure of an angle. This command
rotates the coordinate system that may degrees counter
clockwise about the current origin. his does not affect any
lines that have already been drawn on the page. Example:
90 rotate will rotate the axes 90 degrees
counterclockwise, so the positive y axis now points to the
left, and the positive x axis points up.
number number translate
612 792 translate would move the
origin of the coordinate system to the upper right corner of
the page. Now only points with negative x and y components
will correspond to points on the physical page (assuming an
8.5" by 11" page in the portrait orientation).
number number scale
3 2
scale would cause a line drawn from (0,0) to (72,72) to
appear as if it was drawn from the lower left corner of the
page to a point three inches to the right of the left edge of the
paper and two inches up from the bottom edge of the paper,
assuming the original coordinate system was in effect just
before the command.
number number moveto
72 144 moveto would move the current point
to one inch from the left edge of the paper, and two inches up
from the bottom edge, assuming the original coordinate
system was in effect.
number number rmoveto
moveto, except the numbers specified
give the coordinates of the new current point relative to the
current position. Example: 144 -36 rmoveto would
move the current point set by the previous example two
inches further to the right and one-half inch lower on the
page. Thus the coordinates of the current point become
(216,108). Notice that numbers can be negative!
number number lineto
number number rlineto
lineto, but the coordinates given in the
command are relative o the current position. Again, the end
of the line that is drawn becomes the new current position.
Example: 0 144 rlineto will draw a two inch
horizontal line from the current position two inches to the
right. Using the current position left in the previous example,
this draws a line from (216,144) to (216,288), and leaves the
current point at (216,288).
rotate, translate, or scale commands. That is, each
moveto, rmoveto, lineto, and rlineto command in the
original (input) program should appear in your output (most likely
with modified numbers), but the rotate, translate, and
scale commands in the input must not appear in the output.
Assume the original coordinate system is in effect at the beginning
of execution. The numbers used with the commands in the
program you produce must be accurate to at least two fractional
digits.
Sample solution #2, with matrices
Sample Input
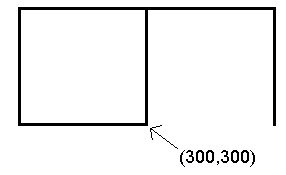
300 300 moveto 0 72 rlineto 2 1 scale 36 0 rlineto 1 -4 scale 0 18 rlineto 1 -0.25 scale 0.5 1 scale 300 300 translate 90 rotate 0 0 moveto 0 72 rlineto 2 1 scale 36 0 rlineto 1 -4 scale 0 18 rlineto *
300 300 moveto 0 72 rlineto 72 0 rlineto 0 -72 rlineto 300 300 moveto -72 0 rlineto 0 72 rlineto 72 0 rlineto
400 500 moveto 300 400 lineto 0.5 0.4 scale 200 200 lineto 95 rotate 250 -200 lineto -100 -100 translate 0.5 0.1 scale 250 70 lineto 250 70 rmoveto 150 250 rlineto *
400 500 moveto 300 400 lineto 100 80 lineto 88.725 106.592 lineto 45.2336 13.2041 lineto -8.93393 49.5657 rmoveto -15.7208 29.0143 rlineto
