
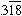
If we are given the decimal expansion of a rational fraction (with an indication of which digits are repeated, if necessary), we can determine the rational fraction (that is, the integer values of p and q in p/q) using the following algorithm.
Assume there are k digits immediately after the decimal point that are
not repeated, followed by a group of j digits which must be
repeated. Thus for 7/22 we would have k = 1 (for the digit 3) and j =
2 (for the digits 1 and 8). Now if we let X be the original number
(7/22), we can compute the numerator and denominator of the
expression:

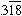 we obtain the following calculation for the
numerator of this fraction:
we obtain the following calculation for the
numerator of this fraction:

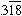 is the decimal expansion of the rational number 315/990.
Properly reduced, this fraction is (as expected) just 7/22.
is the decimal expansion of the rational number 315/990.
Properly reduced, this fraction is (as expected) just 7/22.
The input data for this problem will be a sequence of test cases, each test case appearing on a line by itself, followed by a -1. Each test case will begin with an integer giving the value of j, one or more spaces, then the decimal expansion of a fraction given in the form 0.ddddd (where d represents a decimal digit). There may be as many as nine (9) digits in the decimal expansion (that is, the value of k+j may be as large as 9). For each test case, display the case number (they are numbered sequentially starting with 1) and the resulting rational number in the form p/q, properly reduced.
Sample Input
2 0.318 1 0.3 2 0.09 6 0.714285 -1
Case 1: 7/22 Case 2: 1/3 Case 3: 1/11 Case 4: 5/7