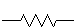
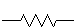
When two resistors are connected in series, as shown below, then their equivalent resistance is just the sum of the resistances of the individual resistors. For example, if the two resistors below had resistances of 100 and 200 Ohms, respectively, then the combined resistance (from point A to point B) would be 300 Ohms. Of course, combining three or more resistors in series would yield a resistance equal to sum of all the individual resistances.

Resistors may also be connected in parallel, like this:

If these two resistors had resistances of 100 and 150 Ohms, then the parallel combination would yield an equivalent resistance between points A and B of

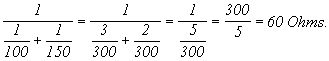
Connecting three resistors in parallel uses the same rule, so a 100 Ohm, 150 Ohm, and 300 Ohm resistor in parallel would yield a combined resistance of just 50 Ohms—that is, 1/(1/100+1/150+1/300) Ohms.

In this problem you're provided one or more descriptions of resistors and their interconnections. Each possible interconnection point (the terminals of a resistor) is identified by a unique positive integer, its label. And each resistor is specified by giving its two interconnection point labels and its resistance (as a real number). For example, the input

1   2   100

would tell us that a 100 Ohm resistor was connected between points 1 and 2. A pair of resistors connected in series might be specified like this:

1   2   100
2   3   200

Here we've got our 100 Ohm resistor connected at points 1 and 2, and another 200 Ohm resistor connected to points 2 and 3. Two resistors in parallel would be similarly specified:

1   2   100
1   2   150

Once you know how the resistors are interconnected, and the resistance of each resistor, it's possible to determine the equivalent resistance between any two points using the simple rules given above. In some cases, that is. Some interconnections of resistors can't be solved using this approach--you won't encounter any of these in this problem, however.

Notes

1. Be aware that there may be input test cases with some resistors that don't contribute to the overall resistance between the indicated points. For example, in the last case shown in the Sample Input section below, the resistor between points 1 and 2 is unused. There must be some flow through a resistor if it is to contribute to the overall resistance.
2. No resistor will have its ends connected together. That is, the labels associated with the ends of a resistor will always be distinct.

Input

Output

Sample Solution

Sample Input

2 1 3 
    1 2 100 
    2 3 200 

2 1 2 
    1 2 100 
    1 2 150 

6 1 6 
    1 2 500 
    1 3 15 
    3 4 40 
    3 5 100 
    4 6 60 
    5 6 50 

0 0 0 

Sample Output

Case 1: 300.00 Ohms
Case 2: 60.00 Ohms
Case 3: 75.00 Ohms

Judge's Input Data