Problem E

Fatman

Some of us may be so fortunate to be thin enough to squeeze through the tiniest hole, others are not. Getting from A to B in a crowded supermarket (even without a cart) can be tough and may require sophisticated navigation: there may seem to be enough room on the one side, but then you may run into trouble with that lady further down...

Let's consider this in an abstract fashion: given an aisle of a certain width, with infinitely small obstacles scattered around, just how fat can a person be and still be able to get from the left side to the right side. Assume that seen from above a (fat) person looks like a circle and the person is incompressible (a person with diameter d cannot go between two obstacles having distance less than d).

Input

The first line of input specifies the number of test cases your program has to process. The input for each test case consists of the following lines:

One line with the integer length L (0 <= L <= 100) and integer width W (0 <= W <= 100) of the aisle, separated by a single space.
One line with the number of obstacles N (0 <= N <= 100) in the aisle.
N lines, one for each obstacle, with its integer coordinates X and Y (0 <= X <= L, 0 <= Y <= W) separated by a single space.

Output

For each test case given in the input, print a line saying 'Maximum size in test case N is M.', where M is rounded to the nearest fractional part of exactly four digits. M is the maximum diameter of a person that can get through the aisle specified for that test case. N is the current test case number, starting at one.

Sample Input

Sample Output

Maximum size in test case 1 is 2.2361.

The sample input looks like:

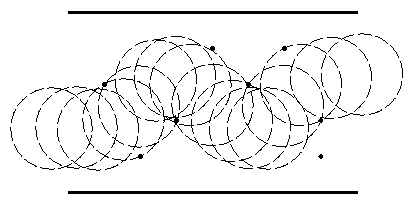
This page maintained by Ed Karrels.
Last updated September 20, 1999