Problem G

Quadtrees

A quadtree is a representation format used to encode images. The fundamental idea behind the quadtree is that any image can be split into four quadrants. Each quadrant may again be split in four sub quadrants, etc. In the quadtree, the image is represented by a parent node, while the four quadrants are represented by four child nodes, in a predetermined order.

Of course, if the whole image is a single color, it can be represented by a quadtree consisting of a single node. In general, a quadrant needs only to be subdivided if it consists of pixels of different colors. As a result, the quadtree need not be of uniform depth.

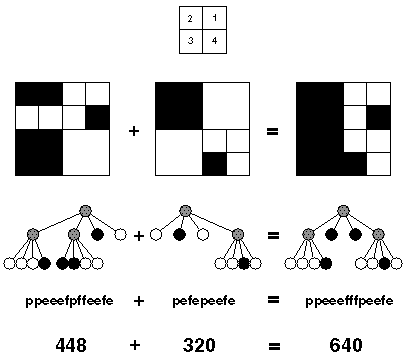
A modern computer artist works with black-and-white images of 32×32 units, for a total of 1024 pixels per image. One of the operations he performs is adding two images together, to form a new image. In the resulting image a pixel is black if it was black in at least one of the component images, otherwise it is white.

This particular artist believes in what he calls the preferred fullness: for an image to be interesting (i.e. to sell for big bucks) the most important property is the number of filled (black) pixels in the image. So, before adding two images together, he would like to know how many pixels will be black in the resulting image. Your job is to write a program that, given the quadtree representation of two images, calculates the number of pixels that are black in the image, which is the result of adding the two images together.

In the figure, the first example is shown (from top to bottom) as image, quadtree, pre-order string (defined below) and number of pixels. The quadrant numbering is shown at the top of the figure.

Input

The first line of input specifies the number of test cases (N) your program has to process. The input for each test case is two strings, each string on its own line. The string is the pre-order representation of a quadtree, in which the letter 'p' indicates a parent node, the letter 'f' (full) a black quadrant and the letter 'e' (empty) a white quadrant. It is guaranteed that each string represents a valid quadtree, while the depth of the tree is not more than 5 (because each pixel has only one color).

Output

For each test case, print on one line the text '

There are
X black pixels.

', where X is the number of black pixels in the resulting image.

Sample Input

3
ppeeefpffeefe
pefepeefe
peeef
peefe
peeef
peepefefe

Sample Output

There are 640 black pixels.
There are 512 black pixels.
There are 384 black pixels.

This page maintained by Ed Karrels.
Last updated September 20, 1999