Not an official ACM page
[ Problem F
| 1998 ACM Finals problem set
| My ACM problem archive
| my home page]
The 1998 22nd Annual
acm
International Collegiate
Programming Contest World Finals
sponsored by IBM
Problem E
Petri Net Simulation
A Petri net is a computational model used to illustrate concurrent
activity. Each Petri net contains some number of places (represented
by circles), transitions (represented by black rectangles), and
directed edges used to connect places to transitions, and transitions
to places. Each place can hold zero or more tokens (represented by
black dots). Here are two examples:
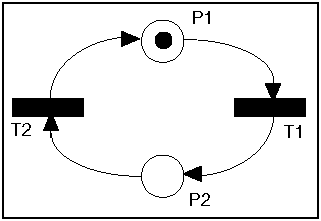
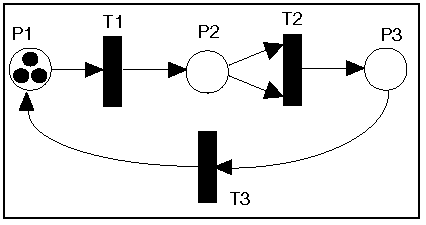
In the first Petri net above, there are two places (P1 and P2) and two
transitions (T1 and T2). P1 initially has one token; P2 has none. P1
is an input place for transition T1, and P2 is an output place for
T1. In the second example there are three places and three
transitions, with three tokens in P1. T 2 has two input places, both
of which are P2.
Operation of a Petri Net
Each transition in a Petri net is either enabled or disabled. A
transition is enabled if there is at least one token in each of its
input places. Any transition can fire whenever it is enabled. If
multiple transitions are enabled, any one of them may fire. When a
transition fires, one token is removed from each of the input places,
and one token is added to each of the output places; this is
effectively done atomically, as one action . When there are no enabled
transitions, a Petri net is said to be dead.
In the top example only T1 is enabled. When it fires one token is
remove d from P1, and one token is added to P2. Then T2 is
enabled. When it fires one token is removed from P2, and one token is
added to P1. Clearly this Petri net will repeat this cycle forever.
The bottom example is more interesting. T1 is enabled and fires,
effectively moving a token to P2. At this point T1 is still the only
enabled transition (T2 requires that P2 have two tokens before it is
enabled). T1 fires again, leaving one token in P1 and two tokens in
P2. Now both T1 and T2 are enabled. Assume T2 fires, removing two
tokens from P2 and adding one token to P3. Now T1 and T3 are
enabled. Continuing until no more transitions are enabled, you should
see that only one token will be left in P2 after 9 transition
firings. (Note that if T1 had fired instead of T2 when both were
enabled, this result would have been the same after 9 firings.)
In this problem you will be presented with descriptions of one or more
Petri nets. For each you are to simulate some specified number of
transition firings, NF, and then report the number of tokens remaining
in the places. If the net becomes dead before NF transition firings,
you are to report that fact as well.
Input
Each Petri net description will first contain an integer NP
(0 < NP < 100) followed by NP integers
specifying the number of tokens initially in each of the places
numbered 1, 2, ..., NP.Next there will appear an integer NT
(0 < NT < 100) specifying the number of
transitions. Then, for each transition (in increasing numerical order
1, 2, ..., NT) there will appear a list of integers terminated by
zero. The negative numbers in the list will represent the input
places, so the number -n indicates there is an input place at
n. The positive numbers in the list will indicate the output
places, so the number p indicates an output place at
p. There will be at least one input place and at least one
output place for each transition. Finally, after the description of
all NT transitions, there will appear an integer indicating the
maximum number of firings you are to simulate, NF. The input will
contain one or more Petri net descriptions followed by a zero.
Output
For each Petri net description in the input display three lines of
output. On the first line indicate the number of the input case
(numbered sequentially starting with 1) and whether or not NF
transitions were able to fire. If so, indicate the net is still live
after NF firings. Otherwise indicate the net is dead, and the number
of firings which were completed. In either case, on the second line
give the identities of the places which contain one or more tokens
after the simulation, and the number of tokens each such place
contains. This list should be in ascending order. The third line of
output for each set should be blank.
The input data will be selected to guarantee the uniqueness of the
correct output displays.
Sample Input
2
1 0
2
-1 2 0
-2 1 0
100
3
3 0
0
3
-1 2 0
-2 -2 3 0
-3 1 0
100
0
Output for the Sample Input
Case 1: still live after 100 transitions
Places with tokens: 1 (1)
Case 2: dead after 9 transitions
Places with tokens: 2 (1)
This page maintained by
Ed Karrels.
Last updated September 8, 1999



