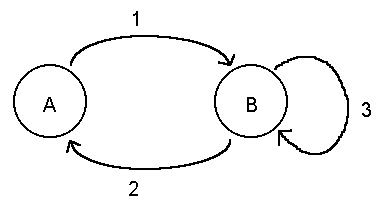
There are two states in this FSM, labeled A and B, and three transitions, labeled 1, 2, and 3. If the current state is A, and the conditions for transition 1 are met, then the current state becomes B. When the current state is B, and the conditions for transition 2 are met, the current states becomes A again. If the current state is B and the conditions for transition 3 are met, the current state remains B.

In this problem the input will be descriptions of several FSMs. Each transition in these FSMs has an associated set of characters called the input set, and a string called the output string. A transition can occur when the current input data character is in the transition's input set. When the transition occurs, the output string is printed.

Input Description

The input consists of a sequence of pairs {FSM description, input for the FSM}. A FSM is described by the following sequence of items separated by whitespace (blanks, tabs, and end of line characters):

• An integer specifying the number of states in the FSM. for each of these states there will be the following items, in order:
  • A one to eight character name for the state. State names are case significant, and unique
  • An integer specifying the number of transitions that leave the current state. For each of these transitions there will be the following data items, in order:
    • The set of input characters that enable the transition (see below). the name of the new current state when this transition occurs
    • The output string (see below).

After the last item in the description of and FSM has been read begin “executing” the FSM using the characters that start on the first complete line following the description. the beginning state will always be called START. The final state will always e called END, but will not appear as a state in the description of a FSM. All input is guaranteed to be correct.

Output Description and Examples

The first example FSM replaces each vowel in a single line of input with an asterisk. The second example will delete each vowel that follows a lower or upper case X, again processing only a single line of input. The final example changes the case of each odd-numbered vowel in the input; processing stops when an exclamation point is encountered, and the remainder of the input line is ignored.

Sample solution

Sample Input

1
START 3
      AEIOUaeiou  START *
      \n          END   \n
      \c          START \c 
This is input for example one.
2
START 3
      \c    START \c
      Xx    SKIP  \c
      \n    END   \n
SKIP  4
      AEIOU START \0
      aeiou START \0
      Xx    SKIP  \c
      \n    END   \n
XaXxe     Test   XIo  iXixO
3
START 12
   \c START \c    !     FINIS \0
   A  TWO   a     E     TWO   e
   I  TWO   i     O     TWO   o
   U  TWO   u     a     TWO   A
   e  TWO   E     i     TWO   I
   o  TWO   O     u     TWO   U
TWO   4
  \c  TWO   \c    AEIOU START \c
   aeiou  START \c  !  FINIS  \0
FINIS 2
   \c  FINIS \0   \n    END   \n
This is some data for FSM number 3.
!    IGNORED
0

Expected Output

Finite State Machine 1:
Th*s *s *np*t f*r *x*mpl* *n*.
Finite State Machine 2:
XXx     Test   Xo  iXx
Finite State Machine 3:
ThIs is sOme dAta fOr FSM numbEr 3.

Judge's Input Data

1
START 2
    \n   END   This_is_the_output_from_the_first_FSM.\n
    \c   START \0
If this appears, the program failed for the first fsm.

1
START 2
    \n   END   Testing\bfor\bproper\bhandling\bof\b\\b\band\b\\\\.\n
    \c   START \0
If this appears, the program failed for the second fsm.

1
START 2
    \n   END   \n
    \c   START \c
The third FSM is correct (it handles \c correctly).

1
START 3
      AEIOUaeiou  START *
      \n          END   \n
      \c          START \c
This is an example from the problem statement, with different text.

2
START 3
      \c    START \c
      Xx    SKIP  \c
      \n    END   \n
SKIP  4
      AEIOU START \0
      aeiou START \0
      Xx    SKIP  \c
      \n    END   \n
XaXxe     Test   XIo  iXixO (This is also from the problem statement).
3
START 12
   \c START \c    !     FINIS \0
   A  TWO   a     E     TWO   e
   I  TWO   i     O     TWO   o
   U  TWO   u     a     TWO   A
   e  TWO   E     i     TWO   I
   o  TWO   O     u     TWO   U
TWO   4
   \c TWO   \c    AEIOU START \c
   aeiou  START \c  !  FINIS  \0
FINIS 2
   \c  FINIS \0   \n    END   \n
This is some data for the FSM. There will be two lines of output.
The last word on this line is FINIS.!    IGNORED.

22
AA 2
   \n   FAIL \0
   \c   AB   T
AB 2
   \n   FAIL \0
   \c   AC   h
AC 2
   \n   FAIL \0
   \c   AD   i
AD 2
   \n   FAIL \0
   \c   AE   s
AE 2
   \n   FAIL \0
   \c   AF   \b
AF 2
   \n   FAIL \0
   \c   AG   F
AG 2
   \n   FAIL \0
   \c   AH   S
AH 2
   \n   FAIL \0
   \c   AI   M
AI 2
   \n   FAIL \0
   \c   AJ   \b
AJ 2
   \n   FAIL \0
   \c   AK   d
AK 2
   \n   FAIL \0
   \c   AL   o
AL 2
   \n   FAIL \0
   \c   AM   e
AM 2
   \n   FAIL \0
   \c   AN   s
AN 2
   \n   FAIL \0
   \c   AO   \b
AO 2
   \n   FAIL \0
   \c   AP   w
AP 2
   \n   FAIL \0
   \c   AQ   o
AQ 2
   \n   FAIL \0
   \c   AR   r
AR 2
   \n   FAIL \0
   \c   AS   k
AS 2
   \n   FAIL \0
   \c   AT   .
AT 2
   \n   END  \n
   \c   FAIL \0
FAIL 1
   \c   END  THIS\bPROGRAM\bFAILED!
START 1
   \c   AA   \0
FAILURE FAILURE BAD!

0

Expected Output from Judged runs

Finite State Machine 1:
This_is_the_output_from_the_first_FSM.
Finite State Machine 2:
Testing for proper handling of \b and \\.
Finite State Machine 3:
The third FSM is correct (it handles \c correctly).
Finite State Machine 4:
Th*s *s *n *x*mpl* fr*m th* pr*bl*m st*t*m*nt, w*th d*ff*r*nt t*xt.
Finite State Machine 5:
XXx     Test   Xo  iXx (This is also from the problem statement).
Finite State Machine 6:
ThIs is sOme dAta fOr the FSM. ThEre wIll be twO linEs of OutpUt.
The lAst word On this lIne Is FINiS.
Finite State Machine 7:
This FSM does work.